ОБО МНЕ


Яна Трифонова
E-mail: ccbukvacc@gmail.com
Владимирская область, Муромский район
Ковардицкая средняя школа
Муромского района
Владимирской области
Сайт школы: https://kovardizi.ucoz.net/
Руководитель: Визавер Маргарита Сергеевна
(учитель математики)

Я учусь в 8 классе. Стараюсь учиться хорошо, чтобы успешно сдать экзамены.
У меня много увлечений. Я очень люблю рисовать, шить и слушать музыку.
А я ещё я очень люблю спорт. До 5 класса занималась гимнастикой. Но после неудачного падения спорт пришлось оставить. Третий год восстанавливаюсь и нахожусь на надомном обучении. Времени хватает и для учёбы, и для творчества.
Хотелось бы иметь в жизни больше впечатлений, эмоций. Надеюсь, смогу осуществить все мои мечты и планы.

В МИРЕ БЕСКОНЕЧНОСТИ



В далёкой волшебной стране жил Мудрый Страшила. Он был умный, добродушный и немного стеснительный.
Множество приключений выпало на долю Страшилы: он нашёл верных друзей, победил в войне с Урфином Джюсом и в конце концов мудро и справедливо правил Изумрудным городом.
Много воды утекло с тех пор. Изнемогая от скуки и безделья, решил как-то Страшила всё в своей стране пересчитать. Любил он пофилософствовать на разные темы и задумался, существует ли в мире самое большое число?
Никто не мог ответить ему на этот вопрос. И вспомнил тогда Страшила про чудесные башмачки, которые могли переносить их обладателя в любой уголок Земли. Надо было только стукнуть каблуком о каблук и назвать место.
Башмачки помогали перемещаться даже во времени. Вот и собрался Страшила отправиться за ответом в Древнюю Грецию.
Попал он в 5 век до н.э. Греческий философ Зенон поделился с ним своими размышлениями о математической бесконечности. Согласно парадоксу, быстроногий Ахиллес никогда не догонит неторопливую черепаху, если в начале движения черепаха находится впереди Ахиллеса. Зенон доказал Страшиле, что когда Ахиллес преодолеет разделяющее их расстояние, черепаха проползёт ещё немного, и так всякий раз до бесконечности.
Заинтересовался Страшила и решил узнать, что же такое бесконечность?
С помощью волшебных башмачков попал он в 4 век до н.э. и познакомился там с Аристотелем. Учёный пришёл к выводу, что Вселенная должна быть конечной. Показывая Страшиле на звёзды, он рассказал о том, что космос состоит из огромной, но конечной сферы с Землёй в центре.
Отправился Страшила дальше. Он узнал, что первым среди древнегреческих ученых, кто применил понятие бесконечности для решения практических задач, был Архимед. Он использовал бесконечный числовой ряд, чтобы найти площадь сегмента параболы. В 3 веке до н.э. Архимед подсчитал, сколько песчинок потребуется, чтобы заполнить вселенную Аристотеля, а в Средние века Аристотеля поддержал Святой Фома Аквинский. В 16 веке польский мыслитель Николай Коперник заявил о том, что Земля – не центр Вселенной. В 17 веке Галилео Галилей размышлял о том, что мир бесконечен, а материя вечна.
Так путешествовал Страшила из века в век и в 19 веке встретил математика Георга Кантора, который поведал ему, что существует множество чисел и более одного бесконечного числа.
Потом перенесли башмачки Страшилу в 1924 год. Познакомился он там с немецким математиком Дэвидом Гильбертом, который придумал известный мысленный эксперимент, чтобы показать, как сложно осознать концепцию бесконечности. Этот эксперимент заключался в том, что в отеле с бесконечным количеством номеров, которые уже заняты, всегда можно обнаружить свободное место, подвинув всех на одну комнату.
Вернулся Страшила домой и отправился в библиотеку Изумрудного города. Там он прочёл, что «Бесконечность – это пространство, не имеющее видимых границ, пределов».

Вышел он в сад отдохнуть и увидел некий сорт цветной капусты. Разглядывая её, он заметил, что часть целого устроена подобно тому, как устроено целое.
И понял правитель Волшебной страны, что бесконечность – это не число, а концепция, идея. Что наибольшего числа не существует. Сколько ни прибавляй к бесконечному, оно остаётся все тем же бесконечным. Можно лишь назвать наибольшее число, которому дали конкретное название. Вот, например, в конце 2018 года американец Патрик Лярош представил научному миру самое большое простое число. Длина его – 24 862 048 символов.
Задумал тогда Страшила открыть следующее наибольшее простое число. Но это уже совсем другая история.



БИНОМ НЬЮТОНА

«Подумаешь, Бином Ньютона» -
Кот промяукал Бегемот
(Он Воланда слуга покорный),
Предсказывая жизни ход.
Все это только подтверждает
Ньютона гений, но давно
Бином известен был в Китае,
Арабы знали про него.
Но обобщил Ньютон решение,
Возвел он в степень многочлен...
Избавил нас от всех сомнений
Других же нет у нас проблем.
Скажите нам совсем без прений
Зачем нам нужен тот бином?
Комбинаторику явлений
Мы без бинома не найдем.
Оскар Хуторянский

подробнее


ТРЕУГОЛЬНИК ПАСКАЛЯ

"Величие человека - в его способности мыслить!"
Блез Паскаль
(1623-1662)


Блез Паскаль – великий математик и физик, замечательный философ, интересный литератор. Биографию этого человека сложно назвать увлекательной, но она довольно необычна. Несмотря на тяжелые болезни, которые сопровождали Паскаля всю жизнь, он оставил после себя немало важных трудов и изобретений. Блез Паскаль стоял у истоков информатики, заложил основы современной теории вероятностей и математического анализа, сформулировал основной закон гидростатики, придумал суммирующую машину, ставшую прототипом калькулятора.
Интересные факты

1
Известный язык программирования «Паскаль» назван в честь создателя первой в мире вычислительной машины.

2
Во время проведения экспериментов с гидростатикой, он разработал и изобрел шприц.

3
Паскаль стал изобретателем обыкновенного устройства, знакомого всем – тачка с двумя ручками и одним колесом.

Чудесный треугольник Паскаля
 "Лестница на гору Меру"Пингала Индия, III век до н.э. Халаюдха Индия, около 975 года Индийский математик Халаюдха написал комментарий к «Чандамшастре» Пингалы, который включает ввод понятия треугольник Паскаля. |  Книга утраченаАль-Караджи Персия, 953–1029 гг. Аль-Караджи написал ныне утерянную книгу, содержащую первую формулировку биномиальных коэффициентов и первое описание треугольника Паскаля. | 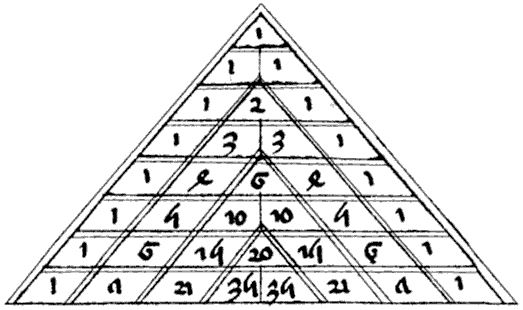 "Треугольник Хайяма"Омар Хайям Иран, около 1100 года Работа Хайяма «Трудности арифметики» была посвящена методу извлечения корней любой степени из целых чисел – «метод индийцев». Этот математический трактат пока не обнаружен. Основываясь на известных фактах, ученые предполагают, что Хайям открыл формулу возведения двучлена a+b в степень n. |  Аль-СамавальИрак, XII в. В гл. I математического трактата «Аль-Бахир фил-джабр», что означает «Блестящая [книга] о науке арифметике» доказывается биномиальная теорема для n = 3, 4, 7, а в п.8 даны формула бинома и таблица нахождения биномиальных коэффициентов для n = 1, 12. |
|---|---|---|---|
 Насир ад-Дин ат-ТусиПерсия, 1265 г. В «Сборнике по арифметике с помощью доски и пыли» ат-Туси подробно описал прием извлечения корней любой степени. Ат-Туси приводит здесь таблицу биномиальных коэффициентов в форме треугольника. |  "Треугольник Яна Хуэйя"Ян Хуэй Китай, 1303 г. Чжу Шицзе Китай, 1303 г. Треугольник изображен на иллюстрации книги «Яшмовое зеркало четырех элементов» китайского математика Чжу Шицзе. В треугольнике записаны биноминальные коэффициенты до седьмой степени включительно. |  Учебник арифметики 1529 г.Петер Апиан Германия, 1529 г. Опубликовал полный треугольник на титульном листе учебника арифметики. |  Михаэль ШтифельГермания, 1544 г. В его главном труде «Полная арифметика» он опубликовал правило образования биномиальных коэффициентов и составил их таблицы до 18-й степени. Таким образом, он составил часть треугольника (от второго до среднего столбца в каждой строке), описав его как таблица фигурных чисел. |
 "Треугольник Тартальи"Никколо Тарталья Италия, 1499-1557 гг. В «Общем трактате о числе и мере» Н. Тарталья опубликовал шесть строк треугольника. Коэффициенты разложения степени бинома расположены вдоль диагонали, соединяющей соответствующие номера строк и столбцов. Таблица была нужна Тарталье для нахождения количества существенно различных выпаданий в случае 1, 2, … игральных костей. |  "Треугольник Паскаля"Блез Паскаль Франция, 1653 (1655) г. Описан в «Трактате об арифметическом треугольнике». Треугольник Паскаля – бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. Числа арифметического треугольника являются числами сочетаний, подсчитываемыми по формуле Ckn = Cn-1k + Cn-1k-1 |  "Треугольник Люка"Франсуа Эдуард Анатоль Люка Франция, XIX в. Суммы чисел, стоящих на восходящих диагоналях, дают последовательность чисел Люка: 1, 3, 4, 7, 11, 18, / которые могут быть определены как Ln=Ln-1+Ln-2, L0=2, L1=1 Каждый элемент треугольника определяется по правилу Паскаля Ln+1,k=Ln,k-1+Ln,k при начальных условиях L1,0=1, L1,1=2 и L0,k=0 т. е. n-я строка треугольника люка может быть получена сложением n-й и (n-1)-й строк треугольника Паскаля. |  "Треугольник Фибоначчи"Леонардо Пизанский (Фибоначчи) Италия, XIII в. Если строки в треугольнике Паскаля выровнять по левому краю, то суммы чисел, расположенных вдоль диагоналей, идущих слева направо и снизу вверх, равны числам Фибоначчи — 1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,…11235813213455891442333776109871597… (каждое число в этой последовательности равно сумме двух предыдущих, а начинают по�следовательность две единицы). |
 "Треугольник Трибоначчи"Леонардо Пизанский (Фибоначчи) Италия, XIII в. Треугольник назван так потому, что суммы элементов, стоящих на восходящих диагоналях, образуют последовательность чисел Трибоначчи: 1,1,2,4,7,13,24,44,..., которая может быть определена следующим рекуррентным соотношением: tn+3 = tn+2 + tn+1 + tn с начальными условиями t0 = 1, t1 = 1, t2 = 2 |  "Треугольник Серпинского"Вацлав Франциск Серпинский Польша, XX в. Если в треугольнике Паскаля все нечетные числа окрасить в черный цвет, а четные — в белый, то образуется треугольник Серпинского. Важным свойством треугольника Серпинского является ег�о самоподобие — ведь он состоит из трёх своих копий, уменьшенных в два раза (это части треугольника Серпинского, содержащиеся в маленьких треугольниках, примыкающих к углам). |  Гуго ШтейнгаузПольша, XX в. Предположим, что вы входите в город как показано на схеме синей стрелкой, и можете двигаться только вперед, точнее, все время выбирая, вперед налево, или вперед направо. Узлы, в которые можно попасть только единственным образом, отмечены зелеными смайликами, точка, в которую можно попасть двумя способами, показана красным смайликом, а тремя, соответственно, розовым. |

Свойства треугольника Паскаля
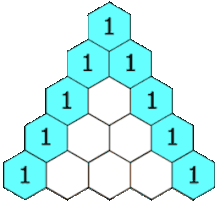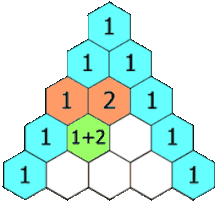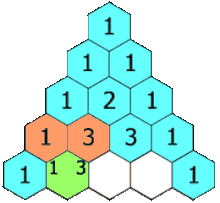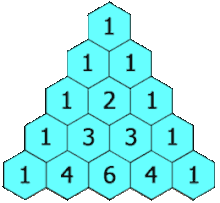
Треугольник Паскаля – арифметический треугольник, образованный биномиальными коэффициентами. Назван в честь Блеза Паскаля, который посвятил ей специальный «Трактат об арифметическом треугольнике».
Если очертить треугольник Паскаля, то получится равнобедренный треугольник. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Продолжать треугольник можно бесконечно. Строки треугольника симметричны относительно вертикальной оси. Имеет применение в теории вероятности и обладает занимательными свойствами:
 |  |  |
|---|---|---|
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |
Слово «бином» означает двучлен – сумма двух слагаемых. Известны формулы сокращенного умножения: (а + b)2 = a2 + 2ab + b2, (a + b)3 = a3 +3a2b + 3ab2 + b3.
Обобщением этих формул является формула, называемая формулой бинома Ньютона:
(a + b)n = C0n anb0+ C1n an-1b + C2n a n-2b2 + ... + Cn-1n abn-1 + Cnn a0bn.
Числа С0n, C1n, ..., Cnn, входящие в формулу, принято называть биномиальными коэффициентами, которые определяются так:
Можно вычислить все биномиальные коэффициенты для любого n путем непосредственного перемножения n множителей (a + b), раскрытия скобок и приведения подобных членов. Правда, математикам древности и средневековья сделать это мешало отсутствие алгебраической символики.


ТРЕУГОЛЬНИК СЕРПИНСКОГО

Вацлав Франциск Серпинский
(14 марта 1882 – 21 октября 1969)
Он был величайшим и наиболее продуктивным польским математиком.
Роткевич Вацлав Серпинский – старейший академик Польши. Он воспитал три поколения учеников, среди которых немало крупных математиков. Его непрерывная творческая деятельность на протяжении шестидесяти лет создала славу польской науке. Серпинский по праву считается отцом польской школы математиков. Автор 724 статей и 50 книг.
Университеты десяти городов: Амстердама, Бордо, Вроцлава, Лакхнау (Индия), Львова, Москвы, Парижа, Праги, Софии и Тарту присвоили Серпинскому степень доктора honoris Kausa. Серпинский – вицепредседатель Международной Академии философии наук, почетный член Болгарской, Итальянской, Лиманской, Парижской, Румынской, Нью-Йоркской, Чехословацкой и других академий науки. Он также почетный член Лондонского математического общества и многих других научных обществ.
Вклад
Вацлава Серпинского
в науку





в сотовых телефонах

в сотовых телефонах

в сотовых телефонах

Капуста Романеско

Лист папоротника

Дерево

Ромашка

Ананас

Подсолнух

Зонтик укропа

Морозный узор

Молния

Побережье Норвегии

Сердечно-сосудистая система

Эйфел�ева башня

Ёлка

Пирамида из детских рисунков

Рождественская ёлка в Риге
 |  |  |
|---|---|---|
 |  |  |
 |  |


Примеры реальных объектов, в орнаментах которых можно заметить фрактал «треугольник Серпинского»

Фрактал, получаемый на основе исследования делимости на 4

Обнаруженные свойства треугольника:
Фрактальная размерность (Треугольник Серпинского состоит из трех копий самого себя, каждая в два раза меньше);
Симметричность (Треугольник симметричен относительно оси равнобедренного треугольника);
Бесконечность (Треугольник можно продолжать до бесконечности).
На цветовой схеме фрактала, получаемого на основе исследования делимости на 4 сохраняется вращательная симметрия 3 порядка. Более сложные степенные структуры появляются со строк с соответствующими номерами: 16 = 42 – со строки n = 16 = 42, 64 = 43 – со строки n = 64 = 43.
Цветовые фрактальные структуры имеют однозначный алгоритм поступательного усложнения. Иначе говоря, эти фракталы остаются детерминистскими (образуются в процессе, называемом итерацией, которая применяет основной рисунок к инициатору, после чего применяет его к результату и так далее).




